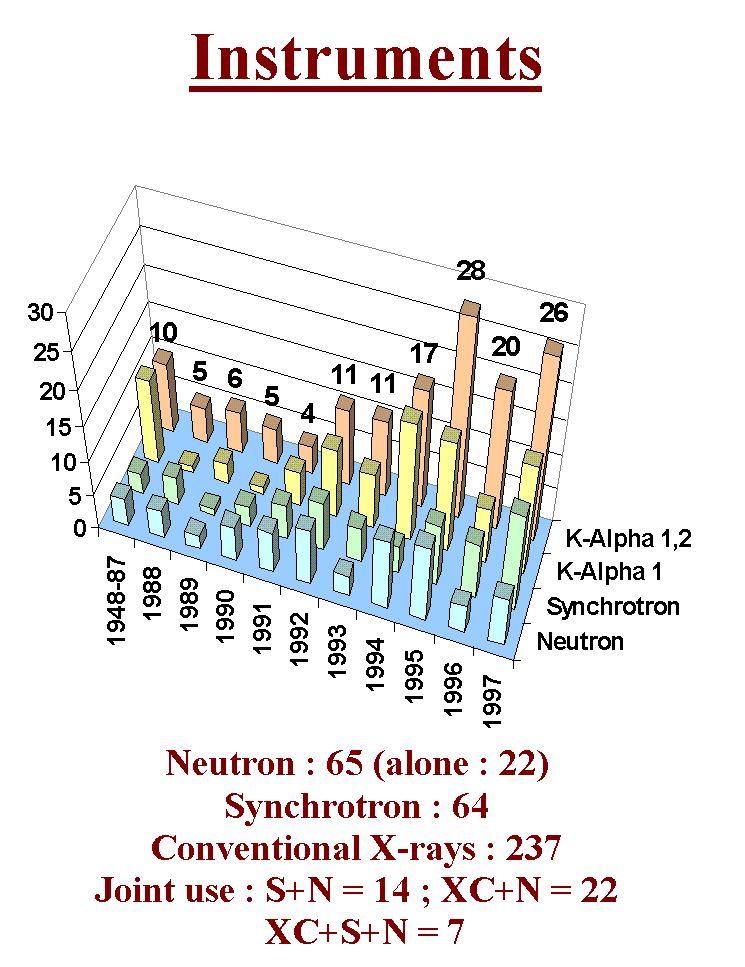

Let us now examine the most classic approach for ab initio structure determination by powder diffractometry : extracting structure factors and solving by Patterson and direct methods. Befor to begin, have a look at the instruments selected for the 300 structure determinations up to the end of 1997. You see the domination of conventional X-rays. I think that the most complex cases will of course be solved by synchrotron radiation but that it will remain a place for solving moderately structures at home.
3.2- Extracting structure factors
Many techniques were used up to now in order to extract structure factors with the target of to determine a crystal structure from powder diffraction data. The simplest technique consists in weighting the intensity by hand. This is possible for isolated reflections. More or less sophisticated methods were applied. Peaks were cutted out of the paper drawing, by chisel, and then the weight of the pieces of paper were measured with a balance ; also, the peak surfaces were carefully measured by a planimeter (a funny surface integrator for which you need good eyes and a stable hand if you expect to be able to reproduce the measurement with accuracy). I did both myself in the past. You can really solve simple problem by these methods. Nowadays, serious pieces of work are undertaken by whole profile analysis. Two approaches have been retained which are distinguishable by the fact that they make use or not of the cell parameters as a constraint for prediction of the angular reflection positions.
3.2.1- Whole pattern refinement without cell constraint
Methods working in this way represent an alternative to the derivative method used for peak position hunting. A by-product is of course the intensity. Profiles of individual reflections were approached by learnt representations (selecting an isolated reflection on the studied pattern or from a standard material) or analytical functions or convolutions of analytical functions (such as Gaussian, Lorentzian, Pearson VII possibly splitted, Pseudo-Voigt, Voigt...).
Some author names have stayed in memory corresponding to a few famous softwares : Taupin (1973), Huang and Parrish (1975) or Will, Sonneveld and Visser (1975)... Some programs are still in use. The main problem of this kind of software is how to make the decision without error about the number of peaks to be included in a compact block of overlapping peaks.
The decision is made either by the user or by an algorithm designed for peak position hunting (eventually by the derivative method). One can imagine the disaster if you need really exactly an estimation for the intensity of each peak.. Indeed, these methods refine the position, the intensity, the width and possibly several profile parameters for each reflection. As a conclusion, the use of these methods should be limited to simple cases, possibly to the estimation of peak positions at low angle for indexation purposes. None of the really complex or moderately complex structures gathered in the SDPD-Databank was solved from structure factors extracted by using these pionneering methods (taking complexity in the sense that many atoms had to be located simultaneously before to be able to start a refinement).
The ultimate evolution of these programs has been to make a list of the starting positions for the peaks to be hunted by using the cell parameters. These softwares are now very similar to those of the next chapter.
3.2.2 Whole pattern refinement with cell constraint
A revolution came with the Pawley method as described in a paper entitled Unit-cell refinement from powder diffraction scans, (G.S. Pawley J. Appl. Cryst. 14 (1981) 357-361). The main purpose was thus clearly to refine cell parameters from the whole pattern, however the possibility to use the extracted intensities as the starting point for the application of direct methods was offered. As well as for the Rietveld method, the Pawley method was not recognized as a revolution for a long time. In the Pawley method, profiles are analytical, their width is constrained to follow a Caglioti law with the three refinable parameters U, V, W as defined in most of the Rietveld-derived softwares. The main difference with the Rietveld method is that the intensities are considered as refinable parameters. Slack constraints were introduced for stabilization of the intensities of those reflections overlapping too much. So, the reflection positions are constrained by the cell knowledge.
The cell parameters can themselves be refined during the process if the user chooses to do so. Taking the case of 1000 reflections as an example, the number of parameters to be refined when applying the Pawley method is near of 1010 (1000 intensities + one to six parameters for the cell + the zeropoint + one or two profile parameters + the U,V,W ones). This leads to a pretty matrix which should be reversed in the refinement process (and consider 10010 for the 10000 reflections of the dreamed synchrotron pattern). The version I tried several years ago was limited to a maximum of 300 reflections on a pattern. I had to cut the pattern into several pieces for complicated crystal structures. Current versions have been improved.
More recently, in 1988, I proposed and applied a different process. The algorithm works by iteration of the Rietveld decomposition formula (which evaluates the so called 'under quotes' observed structure factors "|Fobs|" used in any of the Rietveld programs in order to propose the Bragg reliability factor RB and to allow Fourier syntheses) so that the only parameters refined are the cell and profile parameters (10 to 15 parameters maximum whatever the number of reflections to be extracted). The starting proposition corresponds to a set of reflections as determined by the cell and space group, to which are allocated arbitrarily the same starting intensity (say 100, for instance). The intensities evolve by the simple iterative application of the Rietveld decomposition formula whereas the cell and profile parameters may be refined at each cycle. The "|Fobs|" become the |Fcalc| for the next iteration. With so few parameters, the method is quite fast, stable and efficient. Those reflections which are strictly overlapping are equipartitioned naturally by the process. Efficiency does not mean exactness. One cannot pretend recovering the information definetely lost in powder diffraction due to the monodimensional reduction of data which should be tridimensional for being complete (as it is the case for single crystal four-circle diffractometers data). The quotes in "|Fobs[" meaning that they are not really observed since they are estimated by a process which makes them to depend on the calculated |F| : they are biased, you should be conscious of that.
Nowadays, various modifications of the Pawley and Le Bail methods are in use, representing the main approaches for extracting structure factors from a powder pattern. This is the subject of a talk that will be given at the IUCr Congress, so that I will give you the primer.
Now we come back to our five examples of the tutorial. In the present scenario, the Le Bail method was applied, exclusively.
Na2C2O4
First the sodium oxalate. At this stage, if there is still a doubt about the space group, the best would be to extract the structure factors for each of the space groups remaining in competition. A meticulous examination of the angular ranges where there should be extinction is required. Two different extractions with or without these reflections should lead to some difference allowing to conclude. In the case of the sodium oxalate, the P21/a space group seems the most appropriate and the structure factor extraction is realized. Afterthat we have more than 320 "|Fobs|" at our disposal in the .fou output file from FULLPROF, and we can go to the next step.
[Pd(NH3)4]Cr2O7
After a satisfying structure factors extraction in the P21/c space group, 1054 "|Fobs|" are at our disposal. With a cell volume of more than 1000 A3, we are really outpassing the limits which were previously given for a monoclinic P lattice. Fortunately the presence of heavy atoms (palladium) should facilitate the realization of the next step. Locating them should lead to a minimal starting model allowing refinement and Fourier synthese.
t-AlF3
In the case of the new aluminum fluoiride, by using the more symmetrical space group P4/nmm, 447 "|Fobs|" were extracted up to 145° 2-theta. The cell dimensions suggested 16 formula units per cell. Clearly, the direct methods are adequate for this compound because Al3+ and F- are isoelectronic. The finding of half the independent atoms would not suffice for starting a refinement in such a case very similar to an organic structure problem characterized by the presence of ligth elements only. Almost the whole structure has to be found by the direct methods if one expect to succeed in the structure determination.
beta-BaAlF5
The structure factor extraction in the P21/n generates 1387 "|Fobs|" up to 147° 2-theta. In principle the number of motives per cell is 8 so that 14 atoms in general position have to be located.
Cimetidine C10H16N6S
Extracting structure factors in the P21/n space group provides 924 "|Fobs|". With 4 formula units per cell, the C, N and S atoms represent presumably 17 independent atomic positions at least to be located.
And we could see also the 2 samples of the SDPD Round Robin. But I am afraid that we have no time. I suggest that you give them a look later by yourself.
From this figure, you see that structure determination from powder diffraction data was mainly realized by using direct and Patterson methods. Since a few years, model building is increasingly used. Some structures were guessed, but guessing cannot really be considered as a regular method, for that, you need to have a good nose. We will first examine the classical approach making use of the Patterson and direct methods. Such methods need that you have extracted structure factors.
The choice of the method (direct or Patterson) is suggested by the presence or not of "heavy" atoms. There is no difference here with the strategies recommended for a single crystal study. Here is the list of programs that were used for ab initio structure determination by powder diffractometry. In this scenario were tested the well known programs SHELXS86/SHELX76 (SHELXS86 has been updated and is now inside the SHELX97 package together with an updated version of the SHELXL93 refinement program). You will not find here the manuals of these programs, you will have to read and assimilate them completely, playing with the test files.
At this point of the scenario, the next step is the same one as if we had made the study of a very bad single crystal with a four-circle diffractometer. Indeed, we have quite bad data at our disposal. This is easily understandable. The more a reflection has close neighbouring reflections, the more the "observed" structure factor "|Fobs|" is dubious. In practice, the exact overlapping of two reflections leads to the following proposal : the two reflections have the same structure factor. The Le Bail method applies the Rietveld decomposition formula starting from a set of all identical structure factors, replacing those calculated from a structure model in the normal Rietveld method. As the repartition to the "|Fobs|" in a group of reflections is made according to the |Fcalc|, then two reflections with the same position will receive the same partition and so will remain equal up to the end of the iterative process : this is the so called equipartition. Of course, this is false, however this is the most acceptable proposition we can do at this stage. In fact some programs (as GSAS) offer to start from |Fhkl|s calculated from a dummy atom, this is to be avoided because the strictly overlapping reflections will no be equipartitionned, so that the final dataset will keep some memory of the dummy atom ; moreover, the null reflections will remain at zero after each iteration, even if there is observed intensity (it is thus advised to choose the dummy atom at a general position, not at a special one which could correspond to special extinctions). Maybe it would be possible to redistribute the equipartitionned intensities at a next stage by some special methods proposing to use the information contained in the isolated reflections in order to differenciate the superposed reflections. A less sophisticated means which has proved its utility consists in the elimination of the more dubious reflections from the dataset by using a small software (OVERLAP). If the direct methods are needed, then one should not suppress more than 50% of the reflections. If only few atoms have to be found by the Patterson method then one can suppress more than 50% keeping some chance to obtain the required starting structural model. It would be preferable to associate the criterium for eliminating reflections to the FWHMs rather than to use a fixed proximity value. However the OVERLAP software simply eliminate a reflection if it has a neighbouring one at less than X° 2-theta. If the application of the direct and/or Patterson methods is unsuccessful with the complete dataset, then the game consists in applying them to reduced datasets with X = 0.01 and then 0.02, 0.03, 0.04° 2-theta, etc. Expecting to attain the limits given previously, one should not use X larger than 0.02° 2-theta. There is a list here of other means used for preparing the structure factors, and another list for software allowing to make Fourier synthesis that were used for the previous 300 SDPDs. However, not a lot of people give details about that in their publications.
The optimal conditions for determining a structure from the direct methods correspond to 1 Å resolution (2-theta max ~ 100° for Cu Kalpha wavelength).
Finally, some words about the space group. Sometimes it is really impossible to have a non ambiguous proposition. In the worst cases, several groups may present the same extinctions. Among the possible space groups you should preferably test first the group with the highest symmetry (unless you have external informations, for instance a positive test of acentricity).
We will continue with the scenario samples :
Na2C2O4
No heavy atom in the sodium oxalate, so the direct methods will be applied by the use of SHEXS86 (don't forget to read its manual carefully). In a first approach, the complete dataset (325 "|Fobs|") will be retained. SHELXS86 is started easily in a DOS box, as shown on this figure. Now, have a look at the data file and at the results. The data file is extremely short. The TREF command does all the job. Then, you should take your time and first of all you should compare this result with those obtained from reduced datasets as prepared by the OVERLAP program which is easy to run. Eliminating the reflections having a neighbouring one at 0.02° and 0.04° 2-theta, the remaining reflections are respectively 286 and 242 hkl. The summary of these three attempts corresponding to the five first atoms in the list proposed by SHELXS86 is here. The next step will be the eventual validation of one of these propositions or of some atoms in the list.
[Pd(NH3)4]Cr2O7
For this compound, the Patterson method is the best choice, in principle. Nevertheless the direct methods remain efficient when a small number of atoms have to be found. With SHELXS86, a Patterson followed by an automatic search is much longer in computer time than a direct methods application. That is why my first try is by the direct methods in any case. However for the demonstration purposes, we will follow first the more logical way : the Patterson method. This time, with more than 1000 reflections, and according to the fact that the FWHMs are relatively large, few "|Fobs|" are really well estimated. The Patterson method can be applied from a very limited dataset when the number of "heavy" atoms to be located is small. An application of the OVERLAP program with X = 0.08° 2-theta produces a dataset reduced to 137 reflections. The PATT option of SHELXS86 proposes two atoms : Pd at 0,0,0 coordinates and Cr at 0,0,0.5. The chromium atom being expected in a tetrahedral environment should not occupy an inversion center. We may believe to know the formula and attribute 20 A3 per NH3 group and per oxygen atom : the total is 11x20 = 220 A3 per formula unit to be compared to a cell volume slightly less than 1000 A3 so that the number of formula units per cell could be Z = 4. If the formula is exact, the two sites proposed by SHELXS86 should be two palladium atoms sites. A first refinement (with SHELX76), leads to a result quite unsatisfying with R = 0.62. However the Fourier difference synthesis proposes 2 peaks clearly distinct in weight which could be associated with 2 independent chromium atoms. This hypothesis is tested with SHELX76. The reliability factor goes down to 35% and it seems that the Fourier difference synthesis continue to propose acceptable sites (at least for the three peaks in head of the list) which could correspond to oxygen atoms (being at 1.61 or 1.57 A near of the supposed Cr atoms) or N atoms (being at 2.19 A from a supposed Pd atom). The job consists in introducing the new atoms and to refine until nothing more is recognized on the Fourier difference synthesis.
And what would have given the direct methods ? Application to the 1054 hkl, of which probably no more than 250 are more or less well estimated, proposes randomly the 4 heavy atom sites (2 Pd + 2 Cr) at the head of the list and evenmore !
t-AlF3
The brute force consisting in the SHELXS-97 application to the whole dataset gave a list of 15 atom sites. Examining this list by a structure drawing program (STRUVIR) revealed that the 11 first atom sites described completely a new MX3 corner sharing 3D network. Where is the merit of the researcher ? Thanks to Georges Sheldrick !
beta-BaAlF5
From neutron data, we have no other choice than to apply the direct methods. The more complex case previously solved exclusively from neutron data allowed to locate 6 independent atoms. Here we have 14 sites to locate from low resolution data ! Proceeding meticulously, that's the way. Several datasets were prepared corresponding to different X values in the OVERLAP program. All these datasets were used as hkl files for the direct method application in SHELXS-97. The 14 first peaks of the direct method propositions were introduced into the SHELX76 program, irrespectively of their possible meaning (attributing to all atoms the Ba Fermi length) and a refinement was made on the most reduced dataset (338 hkl corresponding to X = 0.06). Wen all the datasets were treated, curiously, the best proposition (R = 36 %) was obtained from the whole dataset. We may have a look inside the SHELXS-97 proposition. And have a look too inside the SHELX76 refinement result. Looking more accurately to this proposition, it becomes clear that the Q12 site could be an Al atom in octahedral coordination (with Q1, Q3, Q6, Q8, Q9 and Q11 sites as F atoms). The Q13 site presents short distances with Q3, Q4 and Q7 sites, however it is at 2.40 A from Q12 so that it seems to be an artifact. Nevertheless, a structure drawing by STRUVIR is very convincing that at least a large part of the beta-BaAlF5 structure has been obtained. Other interatomic distances could be acceptable as F-F or Ba-F distances. The AlF6 octahedra could not be an artifact, in spite of the fact that a correct proposition from the whole dataset was certainly unexpected due to the low resolution data.
The next step will be obviously to apply the Rietveld method with 13 of the proposed atom sites (excluding Q13). This seems to be a new example that equipartitionning the overlapping reflections produces a random error which does not perturbate the direct methods searching only for order. Of course, solving the structure from the X-ray data was much easier. The two barium atoms only had to be located. They were sufficient to start refinement and find the remaining atoms by Fourier difference synthesis.
Cimetidine C10H16N6S
In the previous structure redetermination from synchrotron powder data (J. Appl. Cryst. 24, 1991, 222-226), the authors input the data extracted by the Pawley method into a number of direct-methods programs, all of which failed to solve the whole structure but correctly located 3 to 4 atoms including the sulfur. The structure was finally solved by taking the top 17 peaks from the output of the direct-methods program SIR.
Here, the 924 reflections extracted by the Le Bail method are used into SHELXS-97 applying the direct methods by the "brute force". The resulting top 17 peaks were introduced into SHELXL for a refinement against a reduced dataset (OVERLAP application with X = 0.03, 378 remaining reflections) more or less irrespective of their physical sense with an exception for the first peak designed as the S atom. A very encouraging R1 ~ 18% was obtained allowing to go further. Examining interatomic distances and the molecule permitted to distinguish between N and C atoms and to attain the next stage consisting in a Rietveld refinement.
All these data are available at the Internet SDPD Web site, if you wish
to try by yourself.
3.4- Strategy for structure completion
Retaining an atom site as proposed by direct or Patterson methods is a question of common sense according to the compound knowledge already at your disposal. You may not have the exact formulation but you should know the composition of the magic pot at the synthesis stage. It is the examination of the interatomic distances which allows you to accept the model or not depending of the atom-types which are probably inside your compound. It may be useful to transfer the atomic coordinates of your model in a program more specialized in interatomic distance calculation than SHELXS86, and eventually in a structure drawing program.
When you believe having obtained a starting model, you have to test the hypothesis by using a single crystal refinement program applied to your "|Fobs|" : the scenario suggests SHELX76 or SHELXL93 and now the SHELX97 package, other are possible. The best approach is to try the proposition on a reduced dataset (apply the OVERLAP software with X = 0.02 or more, depending on your data resolution and on your problem size). A model which corresponds to a reliability R less than 40-35% begin to interest me, a fortiori if peaks extracted from the Fourier difference synthesis make sense. If the peaks pass the test of interatomic distances credibility, they are added to the model as atoms and a new refinement and Fourier synthesis are done (don't be too sure of your sample composition, times to times errors are produced or new reactions take place : Cl atoms enter sometimes in fluorides by the chloride flux method for instance, although this rarely occurs). Once it has become impossible to extract more informations from the "|Fobs|" set (reduced) as resulting from the Le Bail method application, and if the model seems coherent, it is time to apply the Rietveld method. The crystal structure will not be always complete at this first Rietveld method application so that the extraction of new "|Fobs|" at the last Rietveld refinement cycle and their new injection into SHELX76/SHELXL93/SHELX97 (or any single crystal refinement program you may select) will allow to go further if a new Fourier synthesis reveals new sites. Some Rietveld programs have also incorporated Fourier calculations facilities. The process has to be repeated up to complete satisfaction. Results which should be submitted for publication are those of the last refinement by the Rietveld method. Never consider the SHELX result as the final one, the Rietveld method is the only recognized method for powder data refinement ! We will continue with the scenario examples :
Na2C2O4
It is time to examine the 3 propositions from SHELXS86 gathered in naoxa10.html.
In the first proposal corresponding to the complete dataset, the atom noted
1 presents a peak height (474) quite distinct from the others. It could
be a sodium atom, if yes, the atom number 4 at 1.25 Å from the peak
one would be an artifact. Atoms 3 and 2 (with peak height 184 and 251)
would be respectively a carbon and an oxygen atoms or vice versa. The latter
option is more convincing because we expect the carbon atom to be at larger
distance from the sodium atom (distance 2-1 = 3.06 Å) than the oxygen
atom would be (distance 3-1 = 2.26 Å). Something is disturbing in
this first proposition which is the absence of a clear separation between
the peak intensities of what would be atoms and what would be artifacts
(peak number 4). In the second proposition starting from the dataset reduced
to 286 hkl, the peak number 1 would be a C atom, the second peak a Na atom
and peaks 3 and 4 would be oxygen atoms. The third proposition starting
from the 242 hkl reduced dataset is evenmore convincing with peak 1 as
a Na atom, peaks 2 and 4 would be oxygens and peak 3 would be a C atom,
then the intensity decreases abruptly for the fifth peak. Note that proposals
1 and 3 are similar for the three first peaks if peaks 2 and 3 are exchanged.
Entering the four suggested first atoms of proposal 3 into a structure
drawing program like STRUVIR, which also lists interatomic distances, then
a confirmation of the model credibility is obtained. In fact, STRUVIR already
recognizes the presence of NaO6 octahedra (you can visualize
the structure as a 3D model if you have a VRML viewer plugged into you
browser).
With this model, the refinement program SHELX76 is applied on the 242 hkl (the most reduced dataset) and the R factor fall down to 25% after 4 refinement cycles. Looking at the Fourier difference synthesis, nothing more is found. The ultimate confirmation has to be obtained from the Rietveld method. After refinement of a scale factor only, by using the FULLPROF program, keeping fixed the profile parameters as obtained after the Le Bail method application and keeping fixed the structure parameters as refined by SHELX76, one minute later, the model is definetely confirmed by rather low reliability factors. Ultimately, all the refinable parameters are allowed to move by the Rietveld method. The thermal parameters are first refined as isotropic leading to those reliability factors, then they are made anisotropic, this being possible because all atoms are "light" atoms. Finally a preferred orientation is believed to exist in spite of the use of a vertically loaded sample holder (direction [001], March-Dollase parameter of 1.09 indicating in principle needles along the c axis, so that all the other orientations are preferred), we can see the final results. The figure 28 allows to judge of the final refinement quality.
[Pd(NH3)4]Cr2O7
With all the heavy atoms located (Pd and Cr) together with some N and O atoms, a refinement by the Rietveld method is the best thing to do. Reliabilities decrease quickly to RP = 24.6, RB = 20.3, RF = 11.2 % after the FULLPROF application. In order to complete the structure, the "|Fobs|" estimated at the end of the Rietveld method application will be used by SHELX76. We should not forget that in this case we are outside from the theoretical limits so that it could be necessary to use OVERLAP for keeping the less dubious reflections only. In fact, SHELX76 as applied to the 1528 reflections (up to 120° 2-theta) entering the 7 independent atoms yet located allows to get R = 0.109 (corresponding to the RF from FULLPROF). The Fourier difference synthesis is in this case not very well exploited by SHELX76 which does not propose many interatomic distances. It is time to view the structure by STRUVIR and to examine if the new atom sites as proposed by SHELX76 are convincing. The file is quickly prepared, STRUVIR recognizes a complete CrO4 tetrahedron and square planes PdN4 for the two palladium sites. The interatomic distances show that peaks Q1, Q5 and Q7 from the Fourier difference synthesis will constitute acceptable N atoms whereas peaks Q3, Q9, Q11 and Q12 will reasonably correspond to oxygen atoms. One oxygen atom will be lacking at this stage. It will be located after a new FULLPROF-SHELX76 cycle. Its position could have been guessed by the completion of the second CrO4 tetrahedron. Do not expect to locate hydrogen atoms from these data, in presence of the heavy Pd atoms. Nevertheless, not having located them led to a negative thermal parameter for the N atoms in the final refinement (Powder Diffraction, 10, 1995, 159-164).
t-AlF3
The refinement of the positions of the 11 independent atoms as provided by the direct methods leads to the definitive result with Rp = 9.44 % (background subtracted), RB = 4.06 %, RF =3.60 % (provided a preferred orientation is refined in the [001] direction). Further improvement could be obtained when refining anisotropic thermal parameters for all atoms (justified because all atoms are light in this compound).
beta-BaAlF5
The refinement of the positions of the 13 independent atoms by the Rietveld
method leads to RP = 14.3, RB = 11.1 and RF
= 5.5 %. A Fourier difference synthesis made by the SHELX76 program allows
the location of the lacking Al atom well positioned in an AlF6
octahedron. The structure appears now complete as revealed by a STRUVIR
plot, the Q2 and Q5 sites being attributed to Ba atoms. This structure
determination from the low resolution neutron data may looks like a miracle.
Use preferably X-ray data for determining a structure containing heavy
atoms.
Cimetidine C10H16N6S
Introducing the 17 atoms as refined by SHELXL-97 into a Rietveld refinement by FULLPROF led to RP = 12.4 %, RB = 7.73 %, RF = 7.55 %. The C10N6S part of the structure is complete. Comparing with the previously published single crystal data shows that the origin was displaced by 1/2, 1/2, 1/2. Most of the hydrogen atoms are then located by a Fourier difference synthesis realized by SHELXL-97 on the new "|Fobs|" generated by FULLPROF. The best would be to add them in the Rietveld refinement with constraints on C-H and N-H interatomic distances. This synchrotron example does not present FWHMs as low as could be expected from the latest experiments (0.008° 2-theta). The U, V, W profile width values are corresponding to FWHMs as 0.043° 2-theta (at 10° 2-theta), 0.042° (22°), 0.048° (46°), 0.069° (70°). This is not much better than the highest performances attained by the current in-laboratory diffractometers equipped with variable entrance slits. No special difficulty was encountered so that there is no reason for not attempting to solve much more complex structures from synchrotron powder data if really the FWHMs decrease to 0.01° 2-theta. Moreover, there is no reason for not attempting to solve structures as difficult as the cimetidine one from good quality in-laboratory conventional powder diffraction data.
The final Rietveld refinement stage is dominated by two programs essentially. GSAS, with 84 applications and FULLPROF with 57 applications as shown in this list. Five other softwares totalize more than 6 applications, and 20 softwares, whose names are not reported here, were applied 1 to 5 times.
There is a perpetual race for the publication of the most complex structure ever determined from powder diffraction data. The SDPD-Database actually sorts compounds according to 4 complexity criteria. The first of them is the number of independent atoms. Looking at this figure, showing the variation of the maximum and mean values during the last 10 years, one is tempted to conclude that the complexity of structures, which can be determined from SDPD, is slightly increasing.
The second complexity criterion is the number of refined atomic coordinates. The mean value in 1997, near of 50, is almost twice the value observed in the initial 40 years of SDPD. Such an evolution is really expected because of increasing instrumental resolution at synchrotron sources and also in laboratories.
More interesting is the third complexity criterion which is the number of atoms initially located at the first Patterson or direct methods application. The mean is noted M1 here. A partial mean, denoted M2, is also reported, excluding the 100 structures for which 1 or 2 atoms were found to represent a sufficient starting model. In fact, only the maximum shows some tendency to increase but remains rather small, with still less than 20 atoms.
I will now give you some evident reasons for failing : your sample is
a mixture of phases or your data are really too bad versus the problem
complexity. For instance after a dehydration, the crystallinity may remain
too low. Another example where anisotropic broadening effects preclude
to do anything. Even the indexation is highly dubious.