We were up to now in
isotropic microstrain and size approximations. Let us now examine a case
with anisotropic line broadening, a lanthanum-nickel-hydrogen material,
well and long studied by powder diffraction, including various Rietveld
method programs. Each time, the conclusions about anisotropic microstructures
were relatively poor, although taking them into account greatly improved
the fit and the accuracy of the structural parameters. What is really behind
the few values of direction-dependent size and microstrain values produced
by these studies ?

The defects induced by
hydrogen absorption and desorption in the lanthanum-nickel compound were
recently observed by Transmission-Electron-Microscopy, allowing to suggest
what exactly is behind those mysterious root mean square strain and mean
apparent size values estimated from powder data. The electron-microscopy
study evidenced many kind of dislocations (ripple-like, fence-like, misfits,
and loops), also anti-phase boundaries, fracture of slip band structure,
structural disorder and micro-twins. All these defects have effects on
the powder pattern that are gathered in those size and microstrain values.
Progress and innovations in microstructure analysis by the Rietveld method
will never overcome this fact : the powder pattern reveals the whole problem
at a one-dimensional scale, and as a mean.

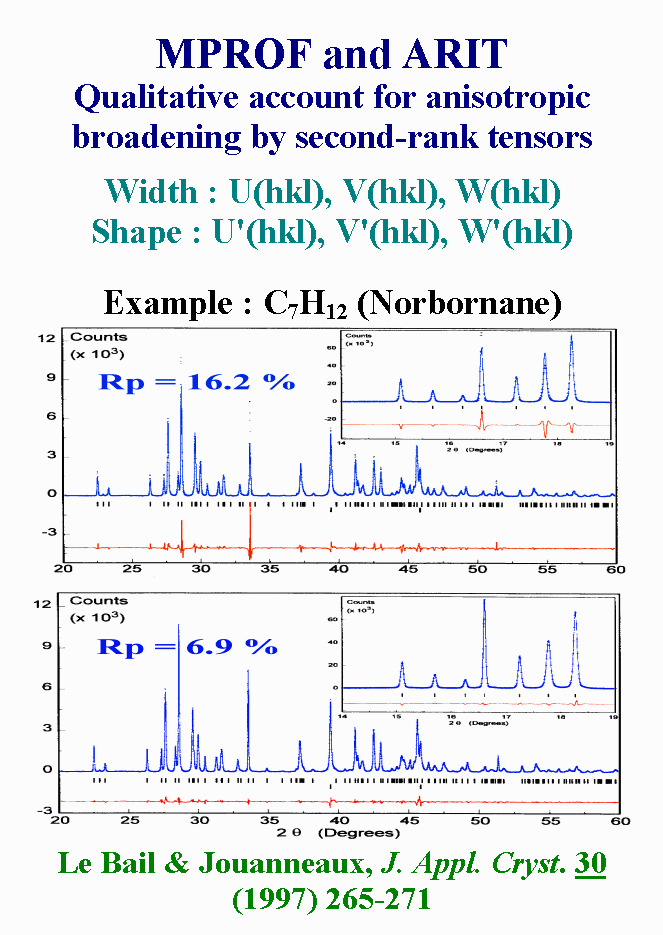
The trend to deal qualitatively
with microstructure effects is illustrated with the case of Norbornane.
Fitting with isotropic line broadening was a kind of disaster. The synchrotron
powder pattern was then fitted with the MPROF Rietveld program, using empirical
simulation of anisotropic line broadening. In this approach, each usual
U, V, and W parameters which describe the peak width and also the peak
shape angular variation, was made hkl-dependent through second-rank
tensors, leading to thirty-six variables maximum in the triclinic case.
The RP value was lowered by almost a factor 2.
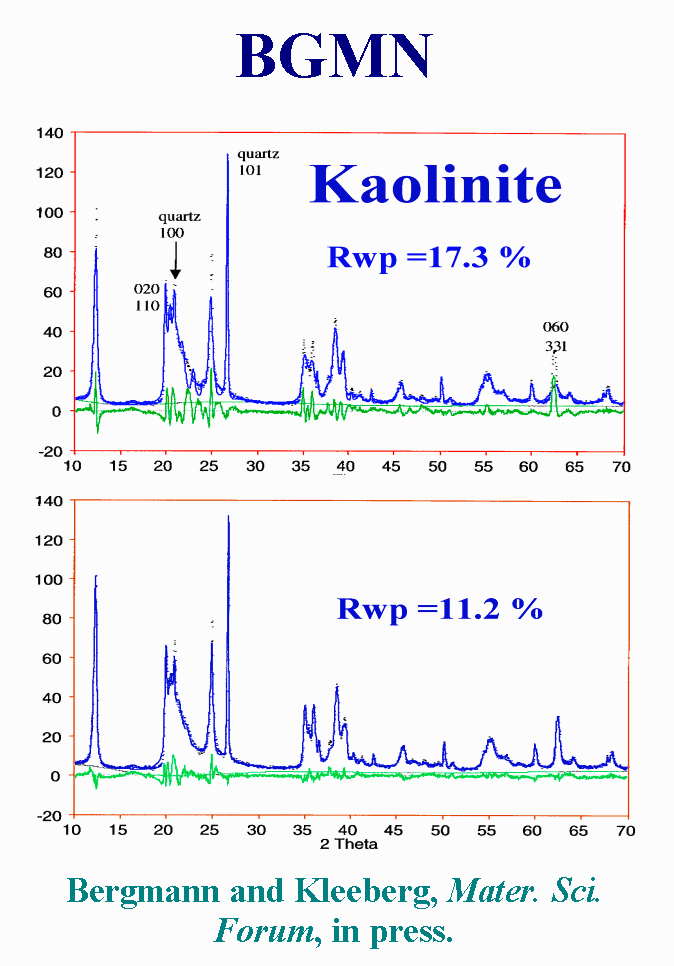
Let us now examine some
complex cases by using one of the most recent Rietveld programs. BGMN is
a commercial package, that is able to behave as an expert system in a few
predefined cases, including stacking faults in disordered layer silicates.
It works by using a Fundamental Parameter Approach for the instrumental
profile. About size-microstrain effects, BGMN uses Lorentzian broadening
(for crystallite size) and squared Lorentzian broadening (for microstrain).
BGMN has default dependence from size/strain. But you may select arbitrary
other dependencies using the built in formula interpreter. This is what
was done for kaolin by introducing a model of disordering : essentially
the pattern is decomposed in 3 sub-phases with different broadening laws.
Yes the fit is improved, but I have not found any size or microstrain or
probability of stacking fault values in the published paper.
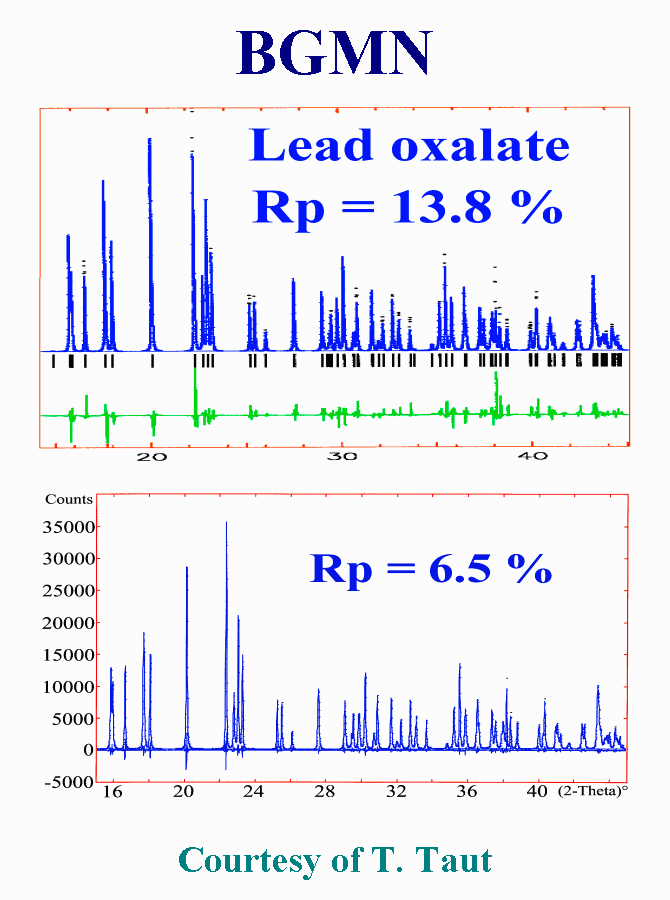
I asked Thomas Taut for
some tests on my two favourite ill-crystallized samples with BGMN. One
is lead oxalate of which the synchrotron pattern is hard to fit due to
stacking faults. BGMN uses ellipsoids as a possibility for anisotropic
effects, but this allowed to decrease the Rp value only by 2 %. Assuming
that there were two slightly different real structures of the same phase,
with nearly the same lattice constants but different peak broadening considerably
improved the fit by BGMN with RP = 6.5 %. The approach is only
qualitative but shows the ease of use of BGMN. In fact the fit was without
the structure constraint, using the Le Bail method I guess, and could not
be realized with the simultaneous refinement of the atomic coordinates.
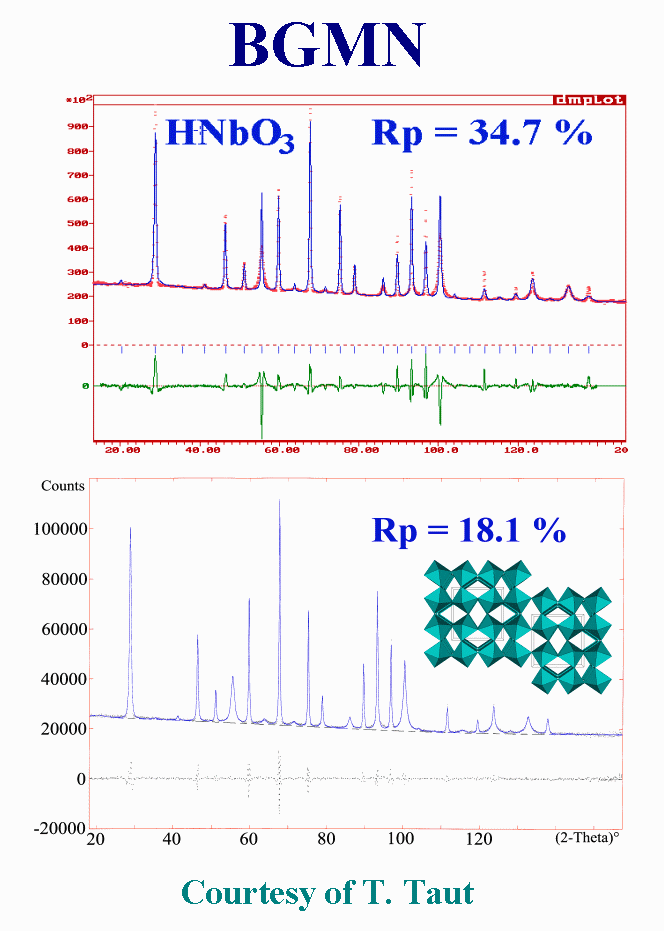
Another highly problematic
powder pattern of a hydrogen niobium oxide was treated with BGMN in a similar
way, using two subphases with different peak broadening, but with less
success, the reliability RP value decreasing from thirty-five
to eighteen percent, which is rather still high. Moreover, because the
individual intensities are arbitrary distributed over the two "phases",
introducing the structure constraint on intensities may alter considerably
the fit quality. Both samples and patterns are challenges for the proposition
of a physically sound model that would allow a satisfying fit by the Rietveld
method, including the structure refinement. The perovskite-type niobium
compound is very probably affected by anti-phase domains extending in the
three dimensions as suggested by this picture.