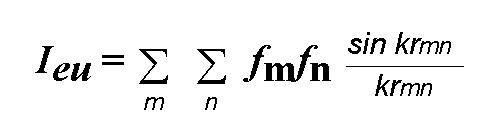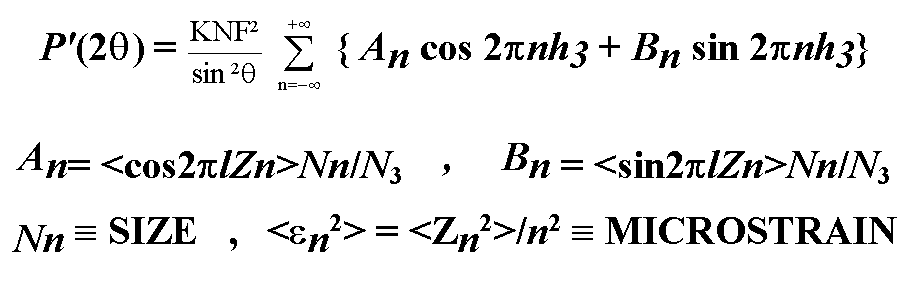THEORY
and PEAK SHAPE MODELS
OLD THEORIES ARE STILL
VALID
No progress in basic powder
diffraction theories on imperfect materials has really emerged since 1950.
THE MOTHER OF POWDER DIFFRACTION
FORMULAE :
The Debye scattering
equation :
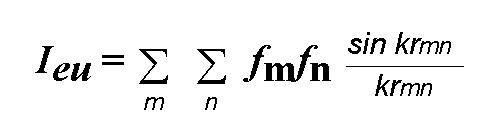
k = 4psinq/l
It involves only the magnitude
of the distances rmn of each atom from every other atom.
Valid for any form of
matter in which there is a random orientation, including gases, liquids,
amorphous solids and crystalline powders :
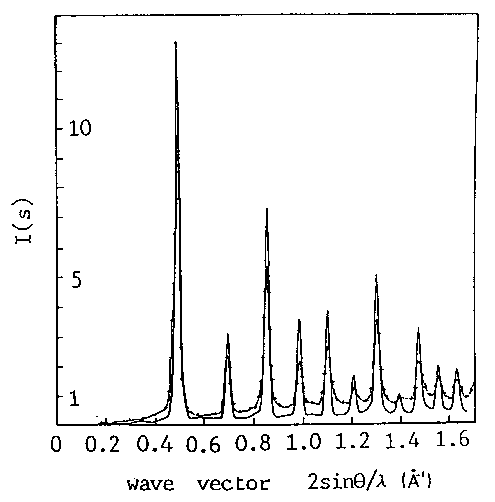
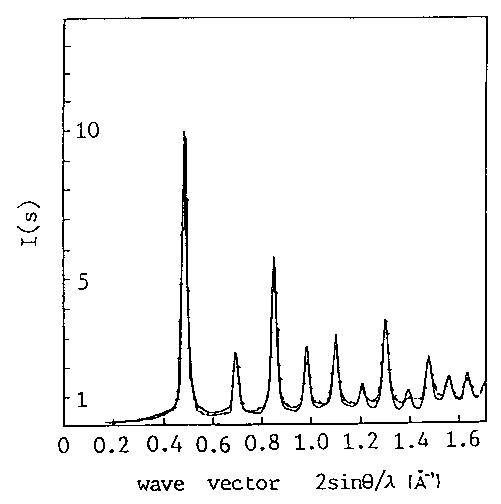
From that formula, you
can calculate the powder diffraction pattern of any model, homogeneous
or inhomogeneous, ordered or disordered.
NOT APPLICABLE TO THE
RIETVELD METHOD
The calculated patterns
were probably (?) estimated by using the Debye scatterring formula.
How would such data be
treated by using the Rietveld method ?
(first, I hope that this
is really f, not h = f *g
i.e. the instrumental
effect was removed or negligible)
One crystalline phase
+ "diffusive" effects included in the background, or
two phases or more, each
of them described from a crystalline model (the core + some boundary models).
Describing defects by
using the hkl-based approach
THE WARREN EQUATION FOR
Size/Microstrain EFFECTS
REMAINS UNDISPUTED :
This equation, expressed
as a Fourier series, provides f for a reflection family
:
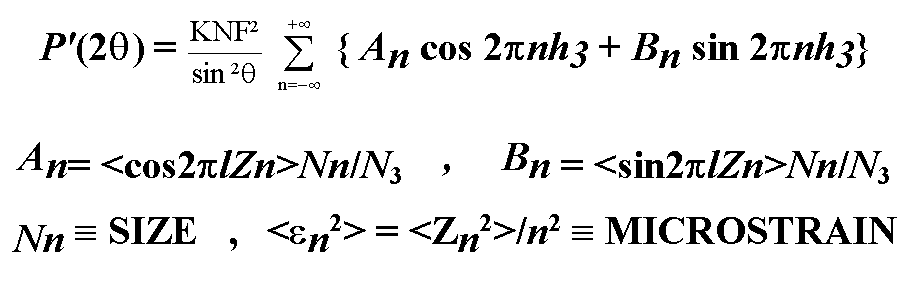
h3 = 2|a3|sin
q/l
Supposes an homogeneous
material.
NOT APPLICABLE AS SUCH
TO THE RIETVELD METHOD.
TOO MUCH UNKNOWNS :
n = 20-100 values
of Nn and Zn for each reflection family.
The need for few parameters
explains why poor restrictive representations of S/M effects were chosen
for f (and h) in WPPF as Gaussian, Lorentzian, Pearson
VII, Voigt, pseudo-Voigt.