

Discovering new allotropic form of any element is always remarkable. It is now rare too to discover new forms of binary compounds. Although 100 or so zeolites are known, a new way to build a 3D four-connected net (in tridimensional AB2 frameworks of AB4 tetrahedra connected exclusively by corners, the A atoms, being connected to 4 other A atoms through the B atoms, lie at the points at a 3D 4-connected net) is of interest a fortiori if the net was not in the list of 1000 or so guessed possibilities built from combinations of previously existing nets. This is why t-AlF3 is distinguished here (t stands for tetragonal in order to avoid confusion with the previously known alpha-, beta- and gamma-AlF3 varieties). The 3D six-connected net family is poor and t-AlF3 represents the ninth recently discovered AB3 framework of AB6 octahedra connected exclusively by corners. Its structure was never predicted. No isotypic coumpound has been prepared to date. It is probably not yet mentioned in any inorganic chemistry book at the AB3 chapter.
The serendipitous discovery of t-AlF3 came from the neutron time-resolved study of the thermolysis of an amorphous AlF3.xH2O (J.L. Fourquet and A. Le Bail, ILL Report, Experiment 5.22.313, 1987, p. 150). The low resolution of the neutron powder pattern did not allow to select a cell among tetragonal and cubic possibilities. Reproducing the experiment by using a limited quantity under an X-ray beam proved to be difficult, the beta-AlF3 form growing first followed by more or less t-AlF3 quantity appearing only after the water complete loss. So the problem stayed unsolved in spite of renewed efforts during several years.

Then t-AlF3 was observed as the thermal decomposition product of [(CH3)4N]AlF4.H2O and a tetragonal cell was evidenced (U. Bentrup, Eur. J. Solid State Inorg. Chem. 29, 1992, p. 51). The compound was almost pure and relatively well crystallized but in powder form only. We made use of the recent development in structure determination from powder diffraction data to solve it ab initio from its X-ray powder pattern. The space group proved to be P4/nmm, with Z=16, a = 10.1843(3) and b = 7.1738(2) Angstroms as refined by the Rietveld method. The direct methods applied to 426 reflections extracted from the powder pattern allowed to locate all the 11 independent atomic sites, as practically required because Al3+ and F- are isoelectronic (A. Le Bail, J.L. Fourquet and U. Bentrup, J. Solid State Chem. 100, 1992, p. 151).
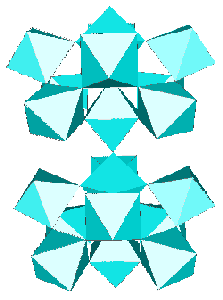
The t-AlF3 structure did not presented new rings of AB6 octahedra. The whole 6-connected 3D net family is built from rings of 3, 4, 5 and 6 octahedra. However, four new building units were inside t-AlF3. The 6 previously known are tetrahedra of octahedra 34 (a geomerical object bounded by 4 triangular faces), prisms with triangular basis 3243 (2 triangular faces and 3 tetragonal faces), tetragonal basis 46 (six tetragonal faces : a cube), pentagonal basis 4552, hexagonal basis 4662 and finally the Friauf polyhedra 3464 characterizing the pyrochlore structure. Only the A atoms at the net points are shown below for the four new building units existing in t-AlF3 :
The t-AlF3 discovery allowed to recognize Na4Ca4Al7F33 (A. Hemon and G. Courbion, J. Solid State Chem. 84, 1990, p. 153) as a stuffed polytype which should be added to the 6-connected 3D net family, the AB3 octahedral framework being [Ca4Al7F33]. Compact clusters of 10 octahedra and even 15 are part of the t-AlF3 and Na4Ca4Al7F33 structures, respectively, they are built exclusively from the 43 units :



As a conclusion, the reality recalls us the inefficiency of our current efforts in order to predict crystalline structures, even relatively simple. We cannot be so sure that rings of 7 or 8 octahedra will never be encountered in the small 6-connected 3D nets family. To obtain new structure-types is easy for quaternary or even ternary coumpounds, but how many will again surprise us with binary formula or how many allotropic forms remain to be discovered for elements ? Even if we could successfully predict them, could we predict how to synthesize them ? A challenge would be to obtain t-ReO3, t-WO3 or t-FeF3, for instance, there is no crystallochemical obstacle to their existence, but how to make them ?!